極大似然估計法的理解指南
今天講一個在機器學習中重要的方法——極大似然估計。
這是一個,能夠讓你擁有擬合最大盈利函數模型的估計方法。
01
什麼是極大似然估計法
極大似然估計是 1821 年由高斯提出,1912 年由費希爾完善的一種點估計方法。
通俗來說,極大似然估計法其實源自生活的點點滴滴,比方說有一個大學生他天天上課不聽講,天天上課玩手機,老師盯着他看了老半天,他也不知道收斂一些,那通過老師幾十年的教學經驗的判斷,這小子期末一定是掛科的,果不其然,他真的掛科了。
老師以過去大量的相同事件來判斷目前正在發生的類似事件,這就是極大似然。
其實一開始寫這個分享,我準備了很多小故事,希望用風趣幽默的文法把一個很抽象的數學名詞儘可能的講給所有人聽,讓大家都能理解並接受。後來我發現,用上面老師和學生的例子是最爲貼切的,因爲也曾經這樣預判過別人。
好啦,故事講完了,接下來就是重頭菜了,原理看着很清晰,但實操起來,需要概率論基礎以及利用微分求極值。
導數
導數的概念的其實挺簡單的,這裏我們不要求掌握太多的關於微積分的公式,只消會求導就可以了,關於基本初等函數的求導,大家可以在這裏查找自己需要的求導公式。
複合函數的求導滿足鏈式法則:
值得一提的還有關於導函數求駐點,即令
,並求解 x,所得到的 x 即爲駐點,駐點回代原函數可得極值。
02
求解極大似然估計量的四步驟
終於到了本文的小高潮,如何利用極大似然估計法來求極大似然估計量呢?
首先我們來看一個例子:有一個抽獎箱,裏面有若干紅球和白球,除顏色外,其他一模一樣。我們每次從中拿出一個後記錄下來再放回去,重複十次操作後發現,有七次抽到了紅球,三次是白球,請估計紅球所佔的比例。
從題目可以分析出本次例子滿足二項分佈,現在可以設事件 A 爲"抽到紅球",那可以得到一個式子:
(1)
現在的目的就是爲了求這個 P(A),那要怎麼求才又快又準呢?如果用求導解駐點來尋找極值,7 次方好像也不是很大,那要是我們重複進行了一百、一千次操作呢?所以,優化算法勢在必行,下面的騷操作就是先輩們經過不懈地探求總結出來的——先取對數再求導!
對(1)式取對數,得:
對上式求導,整理得:
令該導數爲零,可得式子:
解得
從這個例子中我們可以得到和《概率論與數理統計》一書中相匹配的抽象結果:設總體 X 爲離散型隨機變量,且它的概率分佈爲
其中 θ 爲未知參數
和
分別爲 X 的一組樣本和樣本觀察值。則參數 θ 的取值應該使得概率:
達到最大值,今後我們稱 θ 的函數:
爲 θ 的似然函數,上式是其樣本取對應觀察值的概率。同時,如果有
使得:
則稱 爲 θ 的極大似然估計量。從上述一般結果的抽象描述中,我們可以剝離出求解 的一般步驟:
- 寫出似然函數 ;
- 對似然函數取對數(視情況而定);
- 求對數似然函數對未知參數的導函數 ;
- 令導函數爲 0,方程的解即爲極大似然解;
03
基於極大似然原理的 KNN 算法
KNN,即 K-近鄰算法,是極大似然的一個體現,具體思想如下:
首先我們定義一個點,這個點很特別,它具有:
X軸的值
Y軸的值
顏色標籤(這裏我們使用黑、紅、藍三種顏色做個演示)
然後我們多搞幾個點,製造出點羣,也是較爲簡陋的一個數據集
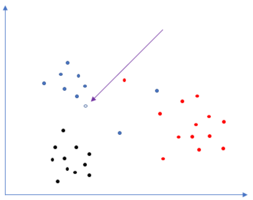
接着有一個不知道自己是啥顏色的小不點溜進來了
現在黑、藍、紅三個點羣展開了激烈的爭論,到底這個小不點是屬於哪一方的!
可是應該如何來判決呢?
小不點想出了一個絕妙的法子,記錄自身到每一個顏色點的距離,然後選取其中 K 個距離值,並以最大的那個距離爲半徑,自身爲圓心,畫一個圓,計算圓內每一個顏色佔總點數的概率,最大概率的那個顏色標籤即是小不點的顏色。
當 k=2 時
當 k=6 時
我們可以發現在有效的K值內,小不點有極大概率是藍色的,因此我們賦予它一個藍色的顏色標籤。至此 KNN 的基本原理已經闡明,該貼一份 C 的 KNN 代碼啦。
但還有一個問題:如何選擇一個最優的 K 值?
這個問題留以後在《基於K-近鄰算法的 KD-tree 詳解》中進行系統的講解,目前一般使用交叉驗證或貝葉斯,先挖個坑在這裏,以後慢慢填啦~
04
KNN 算法的 C 簡單實現
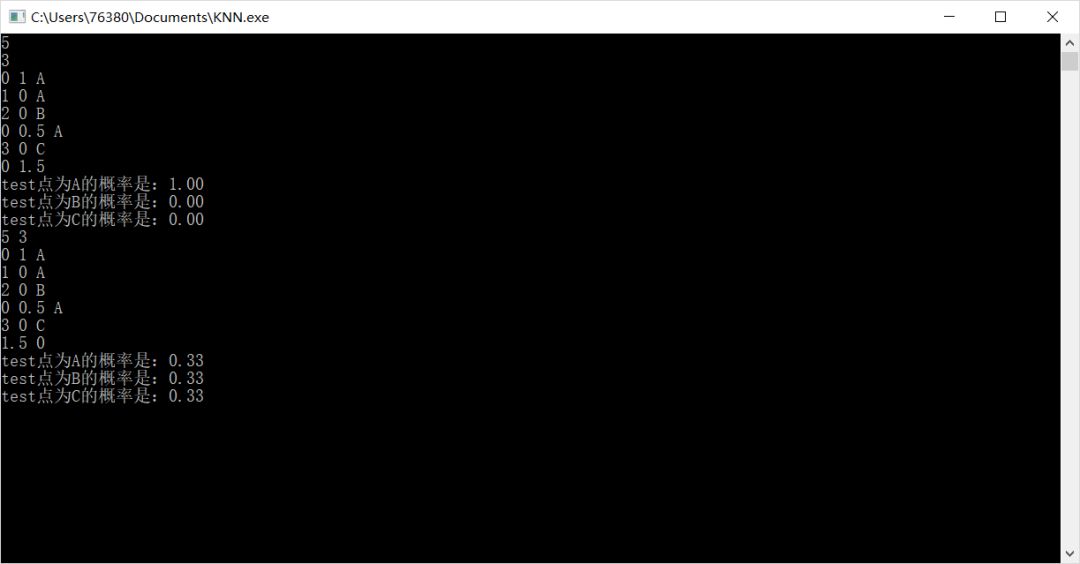
測試圖如下:
KNN 還有更好玩的方法哦,比如 K-D tree,分治思想下的模型,速度更快哦。
參考資料:
《概率論與數理統計》安書田版
維基百科的極大似然估計條目——國內上不了 Wiki 百科,有倆辦法,一個是改 host,另一個你懂的。
CSDN《Markdown 數學符號》——我真的寫這篇被這些數學符號搞得快要原地爆炸了!
作者簡介:
淺淺,目前在閩南師範大學就讀,愛好國學與晨跑,癡迷機器學習與數據挖掘,Lisp愛好者。