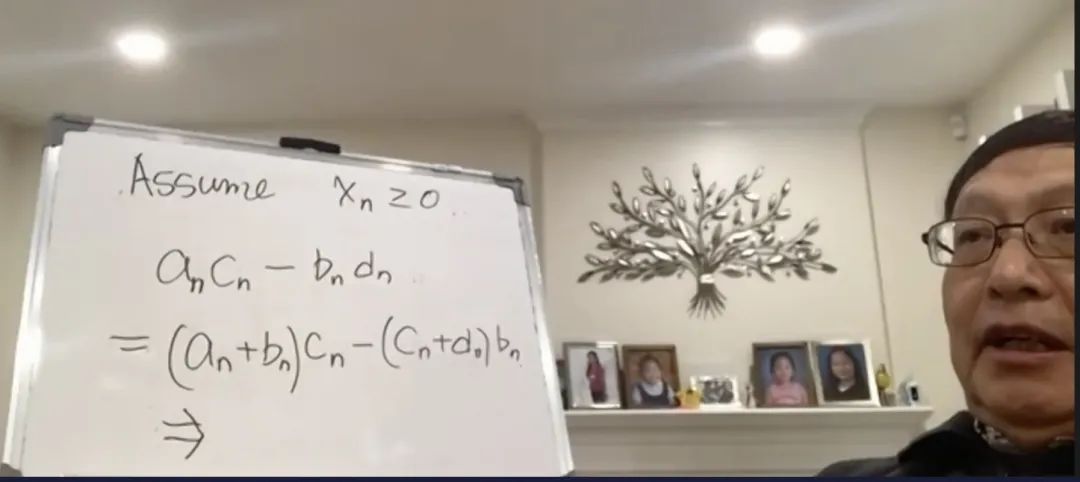歡迎關注“新浪科技”的微信訂閱號：techsina 

來源：新智元

【新智元導讀】關於“零點猜想”問題，大海里的針我沒撈到, 但海底地貌我探得差不多了。

一支馬克筆，一張小白板。

剛剛，張益唐教授現身北大，在B站的直播平臺上，給廣大網友上了一堂大師級數學課。

授課內容大家都知道了，就是最近張教授剛剛取得的新突破：朗道-西格爾零點猜想問題。

這是張益唐親自對自己前不久的那篇論文的全面解析。

全程40分鐘，無廢話無尿點，硬核知識拉滿，信息密度極大。

文字實錄

首先，我得介紹一下這個問題本身。

雖然我的論文已經掛到aXiv上了，但還是得介紹一下：什麼叫朗道-西格爾零點呢？

對於這個狄利克雷L函數，L(s,χ)的原始定義是這樣的：

分子是χ(n)這個值，分母就是n的s次方。

此時，我們只考慮s是個實數的時候，也就是說s=1的時候，它不等於0。那麼s＜1的時候，就是說比1稍微小一點， 它有沒有可能等於0？

這個問題因爲牽扯到很多數論的東西，所以很重要，但始終沒有人能夠解決。

只考慮L(s,χ)不等於0的情況——

如果s比1稍微小一點，這個分母是比較可控的，c是個常數

這是一個猜想，我們說這個猜想比黎曼假設要弱得多，至少是對L函數的黎曼猜想（廣義黎曼猜想）。廣義黎曼猜想是說這個S的實部大於1/2的話不等於0，但就只是很接近1的時候不等於0。

這個猜想本質上說就是朗道-西格爾零點問題。

這個問題，就是要證明這樣的一類零點是不存在的（尤其是實零點，虛零點還容易一點）。

那麼現在我們能做到什麼程度呢？應該說本質上我們至少證明了這樣一個東西

這個2024就像孿生素數里面的情況一樣，是可以改進的。

前兩天消息剛傳出來的時候，很多人不是做數學的，所以不理解這個朗道-西格爾零點問題解決的是什麼，甚至有人以爲就是證明了黎曼假設是錯的。

這個我得說一句：我可沒有這個本事（笑）。我只是在一定範圍內部分地證明了黎曼假設應該是對的。如果說我推翻了黎曼假設，那應該是沒什麼人會相信。

在這篇論文第二節的結尾，我引進了三個proposition，都是不等式。這三個不等式合在一起後，如果說朗道-西格爾零點存在的話，就可以得出一個矛盾。

而這個講起來就是一個非常非常複雜的東西，要講清楚也不容易，但是我可以講一講，這裏面它的一個基本思路，講一下它最後的歸結。最後就是歸結到這樣一個事情上——

怎麼會歸結到這個事情上呢？

對於一個有限的實數序列χn，怎麼樣證明它並不是非負的？

這就是要去證明其中有一個（至少有一個）χn是小於0的。

說起來這個問題是什麼呢？有點不着邊際。

但事實上很有意思，在數論中，特別是解析中，很多東西可以歸結到這麼一個問題。

於是我們就需要發展一個技巧，來證明這個東西是不等於0的。

第一個例子，我們就說一個偶數N（一個比較大的偶數），我們用ρ(n)定義這個素數的特徵函數，都是定義在正整數上。

如果n是素數，ρ(n)等於1，如果n不是素數，ρ(n)就等於0。

就可以得到

我們說這個序列會什麼樣？

一般情況下，它可能等於1，也可能等於0， 但它有沒有可能是負的呢？

很明顯如果ρ(n)是負的，它必須等於-1，而且他負的充要條件是ρ(n)和ρ(N-n)都是素數。這時候χn纔可能是負的，正好等於-1。

很明顯，N永遠是等於n+(N-n)，也就是N就是一個素數加上另外一個素數。

就是說如果在這個序列（1＜n＜N）裏，有某一個χn是小於0的話，充要條件是N是兩個素數的和。

所以哥德巴赫猜想最後就可以歸結到我們來構建這樣一個有限序列，這裏頭是不是有這麼一個小於0的數？如果有的話，哥德巴赫猜想就是對的。

那麼，是不是還有別的問題也是這樣呢？

其實假如我們對孿生素數猜想給出一個弱結果，那麼也會是這樣的，也就是造成這麼一個χn。

它這個定義也是

如果這裏面有兩個是素數，那麼χn就嚴格小於0；如果只有一個素數，那麼就等於0；如果沒有就大於0。

所以在這樣一個序列裏面，我們可以人爲地把n的範圍給它確定，裏面有沒有負的？這就是我們在孿生素數研究下取得的突破。我們的出發點就是這個東西。

話再說回來，怎麼樣去證明某一個χn是小於0，我們就給出了一個很簡單的數列，哪怕裏面有10000個數，我們也可以寫出來這裏面是不是有一個是負的，這很簡單。

但我們這裏考慮的都是理論性的問題，N是一個很大的數，怎麼樣去定義這個東西等於0。

這是第一個例子。實際上它既包括了哥德巴赫猜想，也包括了孿生素數弱結果的研究。

第二個例子是一個純公式的例子，它跟我要做的事情是相關的。

如果有一個Assumption，我們就假定ρ(n+1)>ρn+c——

也就是說零點的間隔比c要大，那麼我們也可以把它歸結成——

其中，f(ρn+a) f(ρn+b)它一定是正的。

爲什麼這麼說呢？因爲隨便一個ρn，從ρn到ρn+c之間，他一定沒有零點。而ρn+a和ρn+b一定在這段之間，因爲f是連續函數，所以他們的乘積一定是大於等於0的。

所以如果我們要證明assumption是不對的，可能有零點的間隔比c要小。如果我能夠證明有一個χn是負的，只要證明它≤0，那這個assumption就錯了。

如果我想證明的話，我就得去弄。

那麼究竟我們需要怎麼處理這個問題呢？

要證明有限的實數序列不是非負的，裏面至少有一個是嚴格小於0的，怎麼去證明呢？

我們常用的處理方法是這樣：

我們找一組新的實數序列{yn}，它要滿足兩個條件。第一：yn≥0，第二個：∑xnyn＜0。只要能找到這樣一組yn，這問題就解決了。

那這裏頭肯定有一項是嚴格小於0的，但yn是大於等於0，那麼xn必須是小於0的。這就解決了傳統要去做的事情。

可是怎麼去選yn呢？這就牽扯到整個篩法發展的歷史了。

最早是挪威數學家Brown在一個世紀前，應該在1917、18年的時候他找到了一組yn。這組yn的表述是很複雜的，但滿足這類條件。

然後他用這個條件能推出9+9，在當時來講是不可思議的，是一個驚人的構造。

後來，到了20世紀40年代末，另外一個挪威數學家叫塞爾伯格，他想得就比較簡單，他說乾脆我就去構造一組實數序列zn，zn是實數就行，沒有任何限制。

然後把yn取成zn平方，於是第一個條件就自然滿足了——實數的平方必然是大於等於0的。

於是問題就變成了，能不能得出下式小於0？

這裏要牽扯到孿生素數猜想最近的進步，特別是梅納德最近的貢獻（他最近得了菲爾茲數學獎）。

xn的取值與孿生數有關，我們希望這裏面至少有一個是負的，然後是求和。

在我之前有三個數學家，他們找到一組zn，能夠證明這個和非常切近0，並且可以做到讓ε任意小。

但是小於0這一步他們怎麼也跨不過去。

而這裏的主要障礙就是，他們要用到素數在等差級數里的分佈，那裏頭有個限制就是有一個exponent指數，它不能超過1/2，否則餘項就控制不住。

於是他們就跨在這個邊上，用他們的話來說差一根頭髮絲就能跨過去了，但這個頭髮絲就沒跨過去。

然後再下一步是我的工作：

我的工作從單獨意義上來講，在等差級數分佈的問題上，應該是第一次突破了指數等於1/2的界限，就是說可以把這個指數取到比1/2再大一點。但我用的zn基本上還是他們引進的。

後來梅納德就把這個問題改進了一大步，他引進了一種新的zn，最後能夠證出這個孿生素數的弱形式，最後我們都是歸結到這樣一個不等式。

下面我們再回到朗道-西格爾零點，

我們也去構造像例2中實的連續函數，如果兩個點中間沒有零點的話，它們就是同號，它們的乘積應該就是非負的。

在論文的引理2.3中，我給出了這麼一個東西，那麼我就是要證明這麼一個事情——

如果存在朗道-西格爾零點，就推出

我想證明這個東西

是錯的，也就是說我能證明

這個裏面有一個是負的話，就可以了。

我花了很長時間，去證明下面這個結果是小於0的。

我找了很多很多這樣的東西，發現一些非常有意思的事情：我沒能直接證明它是小於0的，但我發現對很多zn它接近0。

它會小於一個ε乘上一個東西，而這個ε可以儘量小，我發現很多這樣的zn。所以就差一點。

當孿生素數猜想出來時，有人說我是大海撈針。但實際上不太對，孿生素數實際上我沒有去撈什麼針。

但是去找這個zn，我確實是在大海撈針。

我試了很多很多東西，包括用到像變分法啊，用積分方程去找最大特徵根啊，最後都是有一個問題：你可以在不同角度去找zn，找出來以後都是小於一個ε乘上一個數字，但這個ε你就是跨不過去，有點像我在做孿生素數時那樣。

那最後是怎麼去解決的呢？

這裏我就想提到我在一開始給出的第一個公式。我的一個最初的想法，就是最關鍵的一步，我爲什麼能達到一個這樣的證明。

第一步，我找到兩組序列，都可以寫成是這種形式——

這兩組序列我都可以證明……（這裏還是把它寫出實數形式）

這個東西我不能證明它小於0，實際上嚴格算它就是不小於0，但可以證明它非常接近於0。

同時呢，我也可以證明對於cn和dn，下面這個結果也是接近於0的。

而且呢，證明這兩個關係式雖然看起來結果是一樣的，但證明的方法是完全不一樣的，是兩種完全不同的treatment。

於是，我們又有一種方式證明這個東西接近0，但不能證明它小於0。

那麼這兩組序列有沒有可能發生衝突呢？有衝突，就能給出一個矛盾。於是我就用了這樣一個關係式。

出發點我們還是假定xn大於等於0。

然後我們用這樣一個關係式，也就是一開始寫的那個。

因爲這個χn是非負的，χn我們就不需要取絕對值了。

我們再用這個關係式取一個絕對值，這裏可以全部都取絕對值，減號就變成加號了。

我們有這樣一個關係式，但是我們可以證明，實際上可以假定χn是非負的，我們可以用柯西不等式來估計下面這個的上界。

最後我們發現我們得到一個矛盾（算這個和不如用柯西不等式），我們發現算這個東西是不對的，左邊應該是比右邊的更大，於是用這個方式就推出矛盾來了。

大家有興趣的話可以翻譯一下我這篇文章，在第二節最後，我是用三個proposition就把它給弄下來了，然後剩下的就是去證明那三個proposition。

我們考慮一下數論的歷史，一開始我們總是有這樣的問題，要去構造一個yn。第一個條件是，這個yn必須是非負的，或者什麼樣，然後它乘以χn，加起來要小於0，要去構造這樣一個yn。

最早是Brown在1718年 ，用默比烏斯函數的組合來構造出這樣一個東西。

後來自從Selburg之後，yn就取成zn的平方，這個東西一直沿用下來。

當時我在做孿生素數猜想，我們也知道，yn等於zn平方，它只是一個能夠保證它大於等於0的充分條件，但不是必要條件，還有沒有別的形式 ？

有很多人想過，但目前爲止沒有人想出來（yn不是這個平方的形式）。

在我在這裏，似乎有一種新的辦法（更復雜），實際上我是引進了4個序列。

最後如果這些χn都是大於0，我能推出矛盾來。

今天我就先講到這兒，這個東西作爲介紹性的，我也只能講得比較初等一點。

PS：如有錯誤，歡迎在留言中指正。

論文淺析

在這篇最新的論文中，張益唐教授提出了兩個定理。

第一，對於L(1,χ)的估計：

第二，可能存在的西格爾零點不大於：

其中，c1和c2都是正實數，且與D無關。

論文地址：https://arxiv.org/abs/2211.02515

此前，張益唐教授證明朗道-西格爾零點猜想的論文已經廣泛流傳，由於全篇涉及解析數論等硬核知識，對於廣大網友的理解門檻還是相當高的。

論文公佈之後，來自知乎、B站、微博等媒體平臺的各路專業人士和UP主的解讀也爲數不少了。

比如B站知識區UP“鈺子一”對這篇論文結論的初步解讀：

他的看法是，在假定張益唐教授的證明是正確的情況下（因爲論文目前尚未經同行評議），這篇論文確實是距離證明真正的“零點猜想”最近的一次突破性成果。

下面是真正的“朗道-西格爾零點猜想”：

注意非零域的範圍，最後一項的指數爲-1。

張益唐教授這次在論文中成功證明的定理1和定理2，其中2是1的推論：

可以看到，定理2的最後一項的指數爲-2024，而原始的“零點猜想”的指數爲-1。

換句話說，這是目前關於朗道-西格爾零點猜想問題上，已證結論和待證的“終極目標”之間，距離最近的一次。

張益唐教授在文末表示，這個-2024的指數值，可以取得更大一些，但目前按照論文中的思路，可能取不到-1。

除了熱心網友的粗淺解析，來自山東大學的解析數論專家在“張益唐教授談朗道-西格爾零點猜想研究的新突破”中，也對張益唐教授這次的工作進行了專業角度的解析。

由於全體模D的狄利克雷特徵（Dirichlet character）的適當線性組合，可以表示出模D算術級數的計數函數。因此，狄利克雷L-函數（Dirichlet L-series）與算術級數中的素數分佈問題密切相關。

對於固定的狄利克雷特徵，黎曼ζ函數的解析性質大多容易推廣到相應的狄利克雷L-函數上去。比如當特徵是復特徵時，其L-函數與黎曼ζ函數有類似的非零區域：

但是，當特徵是實原特徵時，在區間

內至多可能存在一個一階實零點，這裏c是一個適當的正常數。

張益唐教授在最新預印本論文裏證明了，模D的實原特徵L-函數在區間

內沒有實零點，這裏c是絕對實效正常數。如果把這裏的2024換成1，就得到原始形式的朗道-西格爾零點猜想。

專家指出，2024雖然大於1，但在數學意義上，與1並沒有實質性的差別。

朗道-西格爾零點猜想

1859年，德國數學家黎曼在論文“論小於給定數值的素數個數”中，首次提及這個猜想。

黎曼發現，質數的分佈跟某個函數有着密切關係：

這個公式中，s是複數，可以寫成s=a+bi這樣的形式（a是s的實部、b是s的虛部、i則是根號負一）。

當s的實部小於1時，整個級數和可能會發散。爲了讓函數適用於更廣的範圍，黎曼把上面的ζ函數改寫爲：

當s爲負偶數（s= -2, -4, -6…）時，黎曼ζ函數爲零。這些s的值，就稱爲平凡零點。

不過，此外還有另一些s的值，能夠讓黎曼ζ函數爲零，它們被稱爲非平凡零點。就是這些非平凡零點，對質數的分佈有着決定性影響。

到了這裏，黎曼本人也無法證明了。

不過他做了一個猜測：黎曼ζ函數所有非平凡零點的實部都是1/2，或者說黎曼ζ函數在1/2<x<1這一區域內沒有零點。這就是黎曼猜想。< font="">

隨後的數學家們，在前人的基礎上繼續前進。

爲此，數學家狄利克雷引入了狄利克雷L函數。

對於這個函數，也有一個猜想：狄利克雷L函數在1/2<x<1這一區域內沒有零點。這就是廣義黎曼猜想。< font="">

倪憶在文章“千呼萬喚始出來，張益唐公佈證明朗道-西格爾零點猜想的論文”中解釋道，如果χ(n)的取值都是實數，那麼L(s,χ)在

裏最多隻有一個零點，而且這個零點一定是實數。這個可能存在的零點被稱爲西格爾零點。而朗道-西格爾零點猜想則斷言，西格爾零點是不存在的。

更確切地說，存在一個正實數c，使得對於任何D和相應的實特徵χ，L(x,χ)在

時都不等於0.

倪憶表示，朗道-西格爾零點猜想是廣義黎曼假設的一種特殊情形，但這是一種非常重要也非常困難的情形。在很多解析數論問題的研究中，都需要把西格爾零點單獨拿出來考慮。

所以一旦證明了朗道-西格爾零點猜想，就可以取得很多新突破，簡化和加強很多經典數論結果。

特別鳴謝：

普林小虎隊“千呼萬喚始出來，張益唐公佈證明朗道-西格爾零點猜想的論文”